Breadth First Search
Given a graph G = (V, E), where V is the set of nodes and E is the set of edges, a breadth-first search (BFS) is a graph traversal algorithm that starts at a given node s of G, and explores all the nodes at distance 1 from s, then all nodes at distance 2 from s, and so on (cf. below).
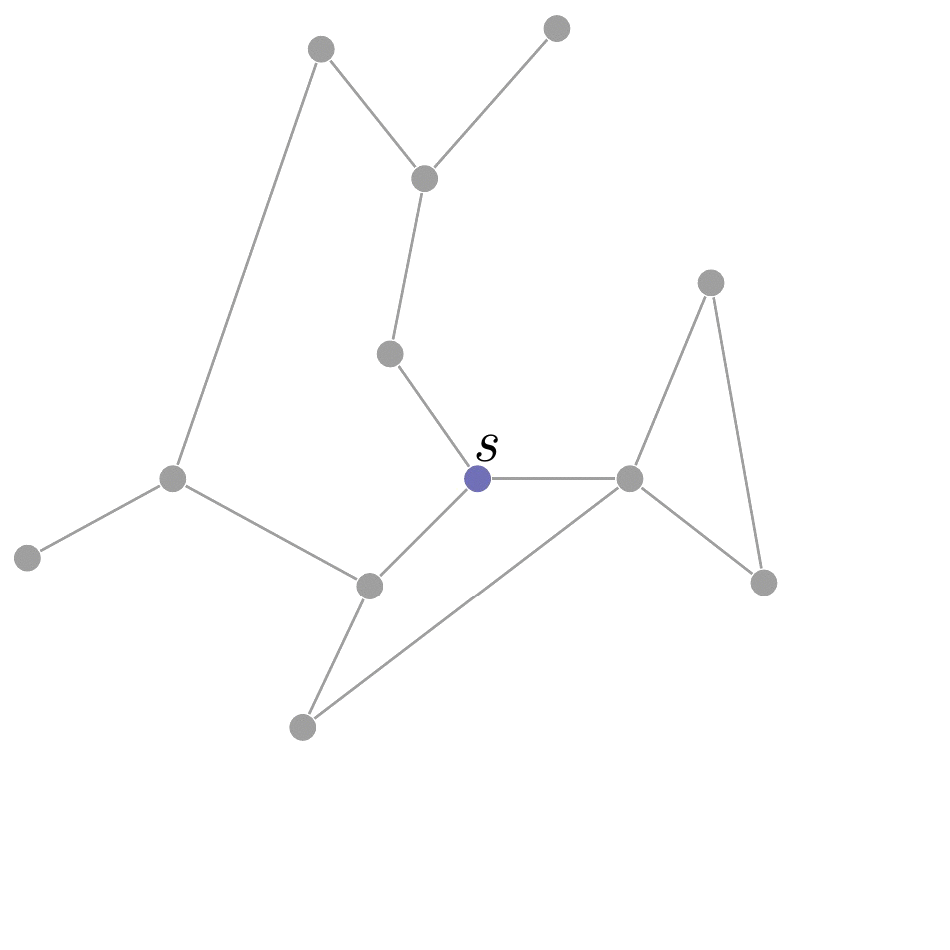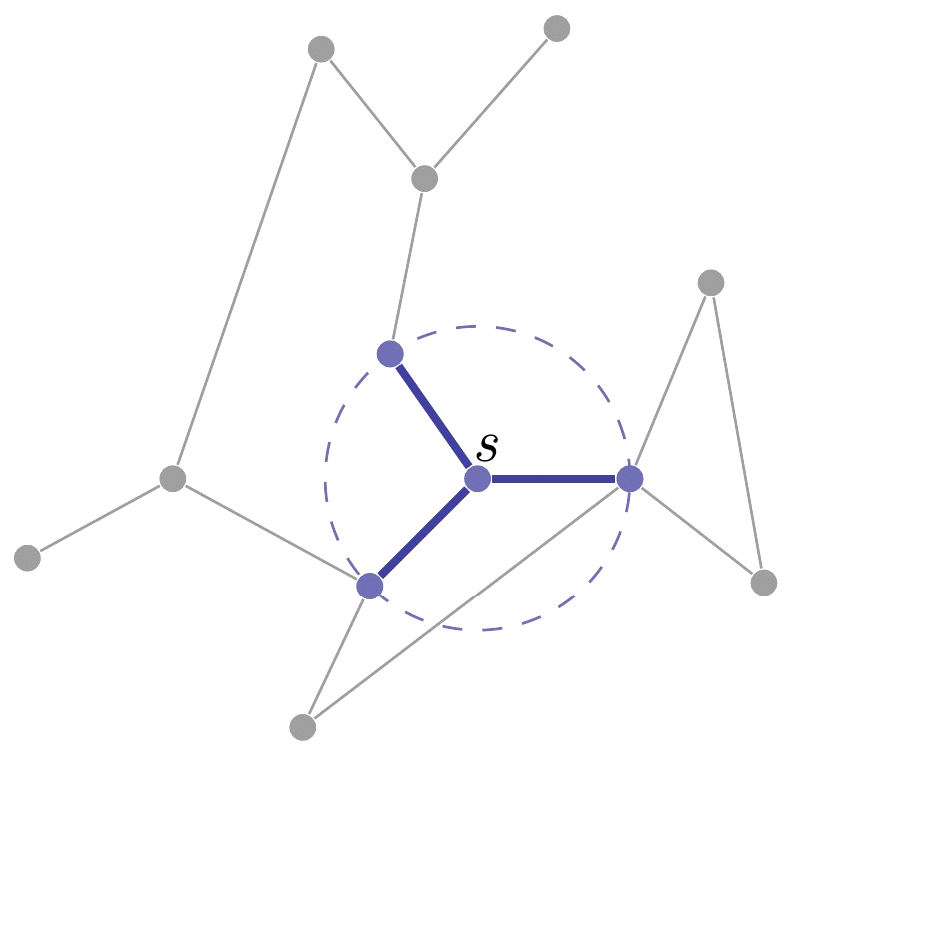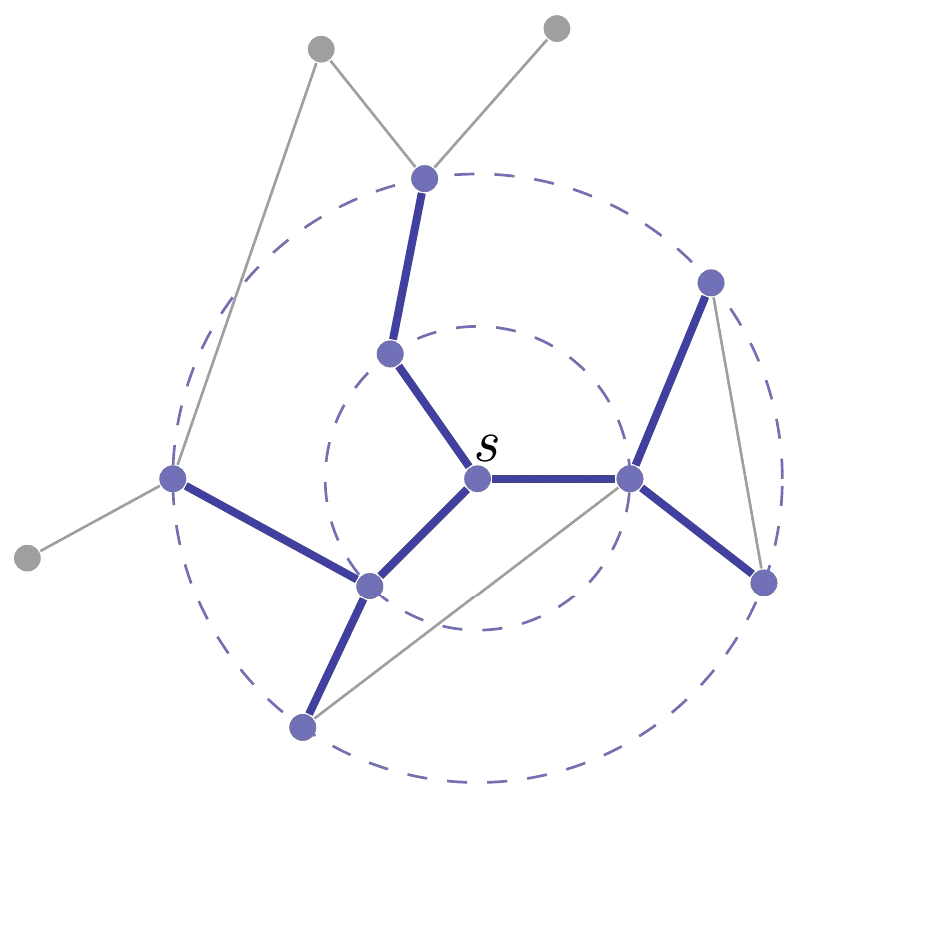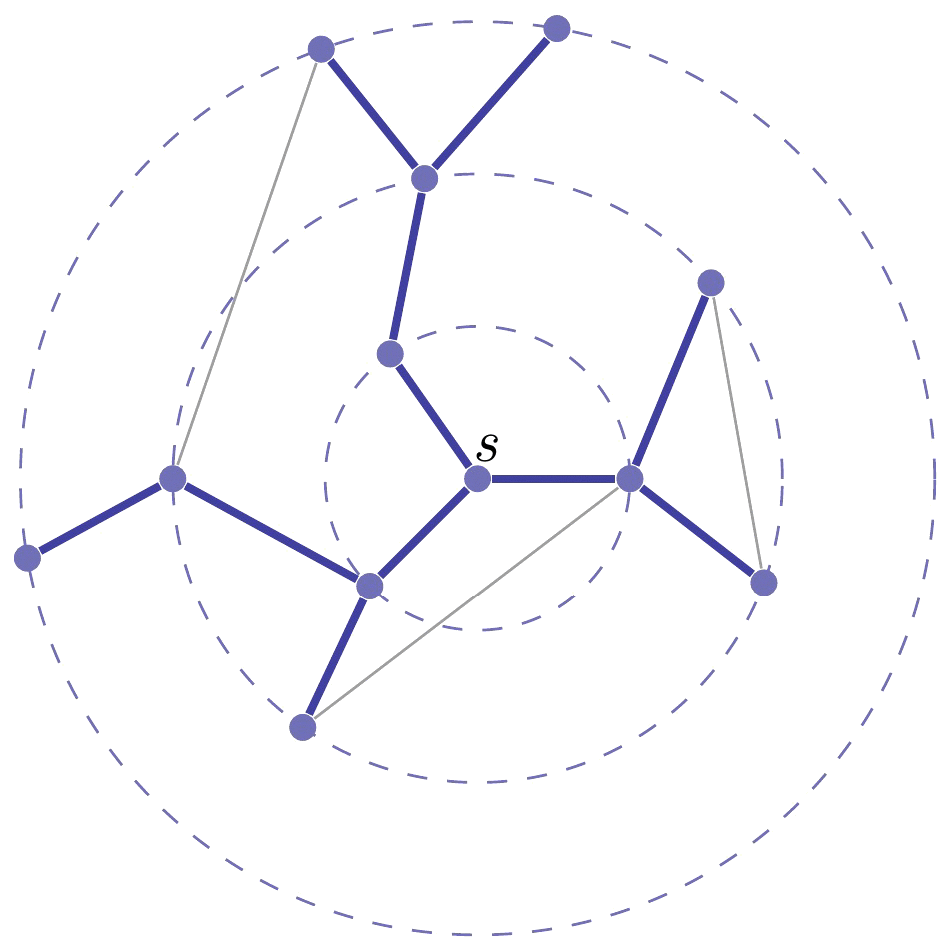
BFS is actually a general search heuristic, not only applied for graph traversal, but also for other problems. Next, we show a toy example, by applying BFS to the subset sum problem.
Subset Sum
Given a set of integers and a target value, find if there is a subset of the given set with sum equal to the given target.
Example
- Input:
numbers = [3, 8, 10, 6, 7],target = 15 - Output:
True - Explanation: The subset
{8, 7}has sum15.
Algorithm
The basic idea is to solve the problem by brute force, i.e., enumerate all the subsets and check if the sum of the subset is equal to the target.
Example
Input: numbers = [3, 8, 10, 6, 7], target = 15
The search tree is as follows:
-
1-element subsets:
[3], [8], [10], [6], [7] -
2-element subsets:
[3, 8], [3, 10], [3, 6], [3, 7], [8, 10], [8, 6], [8, 7], then output[8, 7].
Code
To implement this search process, we need a queue to store the current subset, the current sum and an start index for memorizing the remaining numbers to avoid duplicate combinations.
The queue is initialized with an empty subset. At each step, we pop the first element from the queue, and check if the sum of the subset is equal to the target.
There are threee cases.
- If the sum of the subset is equal to the target. We return the subset and the search process is done.
- If the sum of the subset is greater than the target. We skip the current number.
- If the sum of the subset is less than the target. We format new subsets by adding each of the remaining numbers to the subset, and push them to the queue. Note that the start index of the new subset is the next index of the current number.
We implement the algorithm as follows:
from collections import deque
def subset_sum_bfs(numbers, target):
queue = deque()
queue.append(([], 0)) # (current subset, start index)
while queue:
subset, start = queue.popleft()
current_sum = sum(subset)
if current_sum == target:
return subset
if current_sum > target:
continue
for i in range(start, len(numbers)):
new_subset = subset + [numbers[i]]
queue.append((new_subset, i + 1))
return None