On this page
article
Local Search
Local search is a simple but powerful algorithm. The basic idea is to start with a solution and then iteratively improve it. The improvement is done by trying out different moves. The move that results in the best improvement is chosen.
We use the traveling salesman problem (TSP) as an example to show the power of local search algorithm.
TSP Problem
Given a complete graph G = (V, E) with edge weights d(e) for each edge e ∈ E. Each node represents a city and the edge weights represent the distances between cities. The TSP problem is to find the shortest route that visits all the cities exactly once.

2-OPT
Now we introduce a local search algorithm called 2-OPT to solve the TSP problem. The algorithm is as follows:
- Given a feasible initial solution $s$. Let us denote it by $s={(i_1, i_2), (i_2, i_3), \ldots, (i_n, i_1)}$.
- Define the neighborhood $\delta(s)$ of $s$: For any two arcs $(u, v)$ and $(s, t)$ in $s$, let us consider the solution $s’$ obtained by swapping their connections, i.e., $(u, s)$ and $(v, t)$.

- Search for $s’\in \delta(s)$, if $d(s’) < d(s)$ (where $d(s)$ represents the total length of $s$), then take $s’$ as the new solution.
- Stop when no improvement can be made or when the maximum number of iterations is reached.
- Example
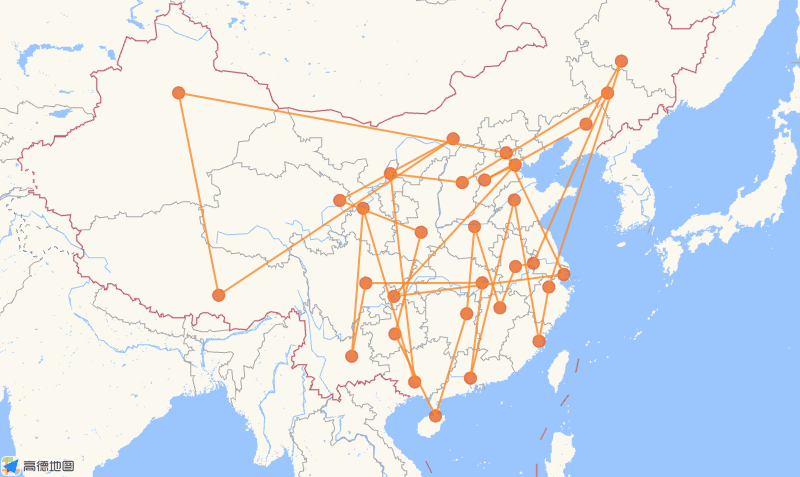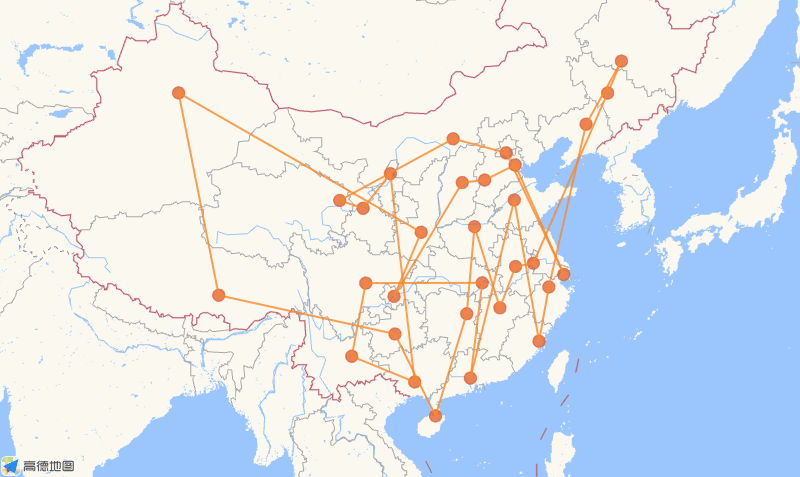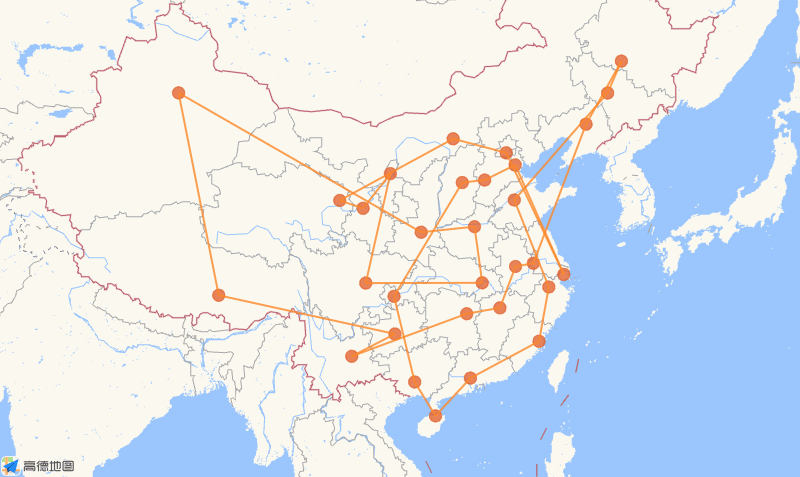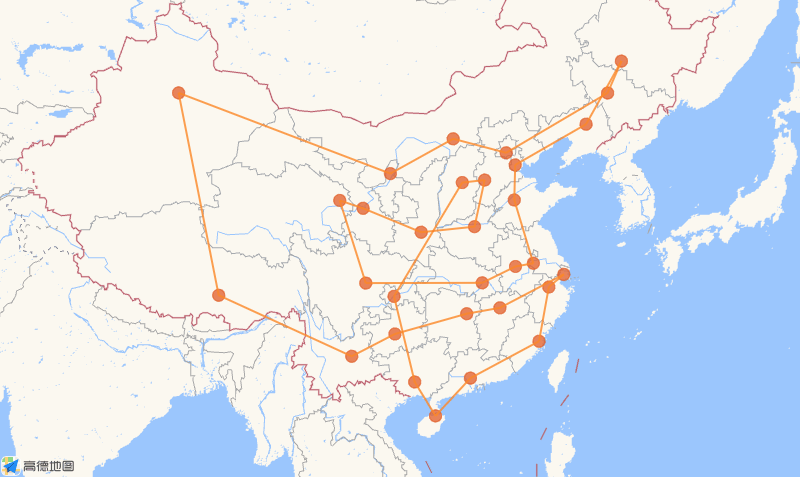
Code
class TSP2opt(object):
max_iter = 10000
def __init__(self, d):
"""
:param d: distance matrix
"""
self._d = d
self._n = len(d)
self._iter = 0
# Start with a trivial solution.
self.tour = [(i, i+1) for i in range(self._n-1)] + [(self._n-1, 0)]
def _2opt(self, i, j):
""" Search with 2opt. If a better solution is found, update the current tour.
:param i: index of the tour, indicating self.tour[i]
:param j: index of the tour, indicating self.tour[j]
:return: True if a better solution is found, False otherwise
"""
u, v = self.tour[i]
s, t = self.tour[j]
part1 = self.tour[0: i]
part2 = [(u, s)]
part3 = [(self.tour[i + j - k][1], self.tour[i + j - k][0]) for k in range(i + 1, j)]
part4 = [(v, t)]
part5 = self.tour[j + 1: ]
new_tour = part1 + part2 + part3 + part4 + part5
new_tour_length = sum([self._d[i][j] for (i, j) in new_tour])
if new_tour_length < self.tour_length:
self.tour = new_tour
return True
return False
@property
def tour_length(self):
return sum([self._d[i][j] for (i, j) in self.tour])
def _print_iter(self):
print(">> iter = %d, tour length = %d" % (self._iter, self.tour_length))
def solve(self):
is_improved = True
while is_improved:
current_length = self.tour_length
for i in range(self._n):
for j in range(i + 1, self._n):
if self._2opt(i, j):
self._iter += 1
self._print_iter()
if self._iter == self.max_iter:
return self
is_improved = current_length - self.tour_length > 0
return self
We may use it in the following way.
import numpy as np
if __name__ == '__main__':
# Generate a random TSP instance.
n = 100 # number of cities
d = np.random.randint(1, 1000, (n, n))
tsp = TSP2opt(d)
tsp.solve()